티스토리 뷰

The Dirac delta or Dirac's delta is a mathematical construct introduced by the British theoretical physicist Paul Dirac. Informally, it is a function representing an infinitely sharp peak bounding unit area: a function δ(x) that has the value zero everywhere except at x = 0 where its value is infinitely large in such a way that its total integral is 1. It is a continuous analogue of the discrete Kronecker delta. In the context of signal processing it is often referred to as the unit impulse function. Note that the Dirac delta is not strictly a function. While for many purposes it can be manipulated as such, formally it can be defined as a distribution that is also a measure.
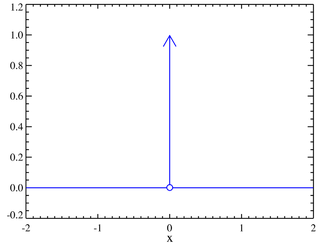
Plot of the Dirac delta function. Schematic representation of the Dirac delta function for x0 = 0. A line surmounted by an arrow is usually used to schematically represent the Dirac delta function. The height of the arrow is usually used to specify the value of any multiplicative constant, which will give the area under the function. The other convention is to write the area next to the arrowhead.
'FINANCE > Financial Enginnering' 카테고리의 다른 글
| [Book] Dynamic Asset Pricing Theory, Third Edition - Darrell Duffie (0) | 2008.06.29 |
|---|---|
| Errata for Stochastic calculus for finance ii (0) | 2008.06.28 |
| Industry |증권사, FICC에 왜 목 매나 (0) | 2008.06.19 |
| [Book] Mathematics of Financial Modeling and Investment Management - Fabozzi, Frank (1) | 2008.06.17 |
| POPTOOLS (1) | 2008.06.16 |
최근에 올라온 글
최근에 달린 댓글
- Total
- Today
- Yesterday
링크
TAG
- 와인
- LG
- 포트폴리오
- VBA
- 세식구
- 리보중단
- Fallback rate
- XAG
- 가을
- 금융수학
- financial
- 유동성최악
- mathematical finance
- RfR
- Risk Free Rate
- SOFR
- random gereragtor
- 꿀떡이
- market convention
- 크레딧투자
- CHF
- 금융공학
- Linear Gaussian Model
- 회고2023
- recession
- JPY
- 어렵다크레딧
- finance
- computational finance
- Volatility Ratio
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 |
| 28 | 29 | 30 | 31 |
글 보관함
